Cauchy distribution
| Probability density function The purple curve is the standard Cauchy distribution |
|
| Cumulative distribution function |
|
| Parameters | 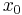 location (real) location (real)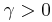 scale (real) scale (real) |
|---|---|
| Support | 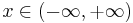 |
![\frac{1}{\pi\gamma\,\left[1 %2B \left(\frac{x-x_0}{\gamma}\right)^2\right]}\!](/2012-wikipedia_en_all_nopic_01_2012/I/110abf1f3bbdd637b6ddd41296caa067.png) |
|
| CDF | 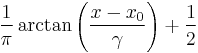 |
| Mean | does not exist |
| Median | 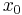 |
| Mode | 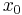 |
| Variance | does not exist |
| Skewness | does not exist |
| Ex. kurtosis | does not exist |
| Entropy | 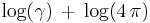 |
| MGF | does not exist |
| CF | 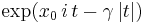 |
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution.
Its importance in physics is the result of its being the solution to the differential equation describing forced resonance.[1] In mathematics, it is closely related to the Poisson kernel, which is the fundamental solution for the Laplace equation in the upper half-plane. In spectroscopy, it is the description of the shape of spectral lines which are subject to homogeneous broadening in which all atoms interact in the same way with the frequency range contained in the line shape. Many mechanisms cause homogeneous broadening, most notably collision broadening, and Chantler–Alda radiation.[2] In its standard form, it is the maximum entropy probability distribution for a random variate X for which 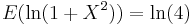 .[3]
.[3]
Contents |
Characterization
Probability density function
The Cauchy distribution has the probability density function
where 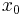 is the location parameter, specifying the location of the peak of the distribution, and
is the location parameter, specifying the location of the peak of the distribution, and 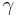 is the scale parameter which specifies the half-width at half-maximum (HWHM).
is the scale parameter which specifies the half-width at half-maximum (HWHM). 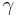 is also equal to half the interquartile range and is sometimes called the probable error. Augustin-Louis Cauchy exploited such a density function in 1827 with an infinitesimal scale parameter, defining what would now be called a Dirac delta function.
is also equal to half the interquartile range and is sometimes called the probable error. Augustin-Louis Cauchy exploited such a density function in 1827 with an infinitesimal scale parameter, defining what would now be called a Dirac delta function.
The amplitude of the above Lorentzian function is given by
The special case when 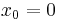 and
and 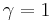 is called the standard Cauchy distribution with the probability density function
is called the standard Cauchy distribution with the probability density function
In physics, a three-parameter Lorentzian function is often used:
where 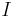 is the height of the peak.
is the height of the peak.
Cumulative distribution function
The cumulative distribution function is:
and the quantile function (inverse cdf) of the Cauchy distribution is
It follows that the first and third quartiles are 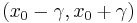 , and hence the interquartile range is
, and hence the interquartile range is 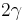 .
.
The derivative of the quantile function, the quantile density function, for the Cauchy distribution is:
The differential entropy of a distribution can be defined in terms of its quantile density,[4] specifically
Properties
The Cauchy distribution is an example of a distribution which has no mean, variance or higher moments defined. Its mode and median are well defined and are both equal to x0.
When 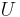 and
and 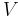 are two independent normally distributed random variables with expected value
are two independent normally distributed random variables with expected value 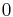 and variance
and variance 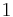 , then the ratio
, then the ratio 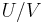 has the standard Cauchy distribution.
has the standard Cauchy distribution.
If 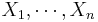 are independent and identically distributed random variables, each with a standard Cauchy distribution, then the sample mean
are independent and identically distributed random variables, each with a standard Cauchy distribution, then the sample mean 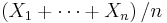 has the same standard Cauchy distribution (the sample median, which is not affected by extreme values, can be used as a measure of central tendency). To see that this is true, compute the characteristic function of the sample mean:
has the same standard Cauchy distribution (the sample median, which is not affected by extreme values, can be used as a measure of central tendency). To see that this is true, compute the characteristic function of the sample mean:
where 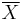 is the sample mean. This example serves to show that the hypothesis of finite variance in the central limit theorem cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all stable distributions, of which the Cauchy distribution is a special case.
is the sample mean. This example serves to show that the hypothesis of finite variance in the central limit theorem cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all stable distributions, of which the Cauchy distribution is a special case.
The Cauchy distribution is an infinitely divisible probability distribution. It is also a strictly stable distribution.[5]
The standard Cauchy distribution coincides with the Student's t-distribution with one degree of freedom.
Like all stable distributions, the location-scale family to which the Cauchy distribution belongs is closed under linear transformations with real coefficients. In addition, the Cauchy distribution is the only univariate distribution which is closed under linear fractional transformations with real coefficients. In this connection, see also McCullagh's parametrization of the Cauchy distributions.
Characteristic function
Let 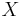 denote a Cauchy distributed random variable. The characteristic function of the Cauchy distribution is given by
denote a Cauchy distributed random variable. The characteristic function of the Cauchy distribution is given by
which is just the Fourier transform of the probability density. The original probability density may be expressed in terms of the characteristic function, essentially by using the inverse Fourier transform:
Observe that the characteristic function is not differentiable at the origin: this corresponds to the fact that the Cauchy distribution does not have an expected value.
Explanation of undefined moments
Mean
If a probability distribution has a density function f(x), then the mean is
The question is now whether this is the same thing as
If at most one of the two terms in (2) is infinite, then (1) is the same as (2). But in the case of the Cauchy distribution, both the positive and negative terms of (2) are infinite. This means (2) is undefined. Moreover, if (1) is construed as a Lebesgue integral, then (1) is also undefined, because (1) is then defined simply as the difference (2) between positive and negative parts.
However, if (1) is construed as an improper integral rather than a Lebesgue integral, then (2) is undefined, and (1) is not necessarily well-defined. We may take (1) to mean
and this is its Cauchy principal value, which is zero, but we could also take (1) to mean, for example,
which is not zero, as can be seen easily by computing the integral.
Because the integrand is bounded and is not Lebesgue integrable, it is not even Henstock–Kurzweil integrable. Various results in probability theory about expected values, such as the strong law of large numbers, will not work in such cases.
Higher moments
The Cauchy distribution does not have moments of any order. This follows from Hölder's inequality which implies that higher moments diverge if lower moments do. In particular, no second central moment exists, as can be verified by direct computation:
The variance does not exist because of the divergent mean, which is distinctly different from having an infinite variance.
Estimation of parameters
Because the mean and variance of the Cauchy distribution are not defined, attempts to estimate these parameters will not be successful. For example, if N samples are taken from a Cauchy distribution, one may calculate the sample mean as:
Although the sample values 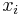 will be concentrated about the central value
will be concentrated about the central value 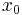 , the sample mean will become increasingly variable as more samples are taken, because of the increased likelihood of encountering sample points with a large absolute value. In fact, the distribution of the sample mean will be equal to the distribution of the samples themselves; i.e., the sample mean of a large sample is no better (or worse) an estimator of
, the sample mean will become increasingly variable as more samples are taken, because of the increased likelihood of encountering sample points with a large absolute value. In fact, the distribution of the sample mean will be equal to the distribution of the samples themselves; i.e., the sample mean of a large sample is no better (or worse) an estimator of 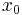 than any single observation from the sample. Similarly, calculating the sample variance will result in values that grow larger as more samples are taken.
than any single observation from the sample. Similarly, calculating the sample variance will result in values that grow larger as more samples are taken.
Therefore, more robust means of estimating the central value 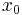 and the scaling parameter
and the scaling parameter 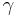 are needed. One simple method is to take the median value of the sample as an estimator of
are needed. One simple method is to take the median value of the sample as an estimator of 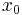 and half the sample interquartile range as an estimator of
and half the sample interquartile range as an estimator of 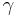 . Other, more precise and robust methods have been developed [6][7] For example, the truncated mean of the middle 24% of the sample order statistics produces an estimate for
. Other, more precise and robust methods have been developed [6][7] For example, the truncated mean of the middle 24% of the sample order statistics produces an estimate for 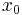 that is more efficient than using either the sample median or the full sample mean.[8][9] However, because of the fat tails of the Cauchy distribution, the efficiency of the estimator decreases if more than 24% of the sample is used.[8][9]
that is more efficient than using either the sample median or the full sample mean.[8][9] However, because of the fat tails of the Cauchy distribution, the efficiency of the estimator decreases if more than 24% of the sample is used.[8][9]
Maximum likelihood can also be used to estimate the parameters 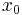 and
and 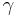 . However, this tends to be complicated by the fact that this requires finding the roots of a high degree polynomial, and there can be multiple roots that represent local maxima.[10] Also, while the maximum likelihood estimator is asymptotically efficient, it is relatively inefficient for small samples.[11] The log-likelihood function for the Cauchy distribution for sample size n is:
. However, this tends to be complicated by the fact that this requires finding the roots of a high degree polynomial, and there can be multiple roots that represent local maxima.[10] Also, while the maximum likelihood estimator is asymptotically efficient, it is relatively inefficient for small samples.[11] The log-likelihood function for the Cauchy distribution for sample size n is:
Maximizing the log likelihood function with respect to 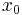 and
and 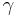 produces the following system of equations:
produces the following system of equations:
Note that ![\sum_{i=1}^n \gamma^2 / (\gamma^2 %2B [x_i - \!x_0]^2)](/2012-wikipedia_en_all_nopic_01_2012/I/0307ec067bb2b9d9be46c04acad0093a.png) is a monotone function in
is a monotone function in 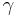 and that the solution
and that the solution 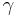 must satisfy
must satisfy 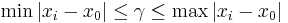 . Solving just for
. Solving just for 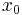 requires solving a polynomial of degree 2n − 1,[10] and solving just for
requires solving a polynomial of degree 2n − 1,[10] and solving just for 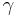 requires solving a polynomial of degree
requires solving a polynomial of degree  (first for
(first for 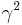 , then
, then 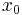 ). Therefore, whether solving for one parameter or for both paramters simultaneously, a numerical solution on a computer is typically required. The benefit of maximum likelihood estimation is asymptotic efficiency; estimating
). Therefore, whether solving for one parameter or for both paramters simultaneously, a numerical solution on a computer is typically required. The benefit of maximum likelihood estimation is asymptotic efficiency; estimating 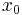 using the sample median is only about 81% as asymptotically efficient as estimating
using the sample median is only about 81% as asymptotically efficient as estimating 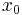 by maximum likelihood.[9][12] The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator of
by maximum likelihood.[9][12] The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator of 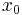 as the maximum likelihood estimate.[9] When Newton's method is used to find the solution for the maximum likelihood estimate, the middle 24% order statistics can be used as an initial solution for
as the maximum likelihood estimate.[9] When Newton's method is used to find the solution for the maximum likelihood estimate, the middle 24% order statistics can be used as an initial solution for 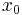 .
.
Circular Cauchy distribution
If X is Cauchy distributed with median μ and scale parameter γ, then the complex variable
has unit modulus and is distributed on the unit circle with density:
with respect to the angular variable 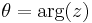 , where
, where
and  expresses the two parameters of the associated linear Cauchy distribution for x as a complex number:
expresses the two parameters of the associated linear Cauchy distribution for x as a complex number:
The distribution  is called the circular Cauchy distribution [13][14] (also the complex Cauchy distribution) with parameter
is called the circular Cauchy distribution [13][14] (also the complex Cauchy distribution) with parameter 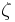 . The circular Cauchy distribution is related to the wrapped Cauchy distribution. If
. The circular Cauchy distribution is related to the wrapped Cauchy distribution. If 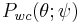 is a wrapped Cauchy distribution with the parameter
is a wrapped Cauchy distribution with the parameter 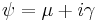 representing the parameters of the corresponding "unwrapped" Cauchy distribution in the variable y where
representing the parameters of the corresponding "unwrapped" Cauchy distribution in the variable y where 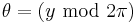 , then
, then
See also McCullagh's parametrization of the Cauchy distributions and Poisson kernel for related concepts.
The circular Cauchy distribution expressed in complex form has finite moments of all orders
for integer 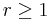 . For
. For 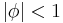 , the transformation
, the transformation
is holomorphic on the unit disk, and the transformed variable 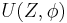 is distributed as complex Cauchy with parameter
is distributed as complex Cauchy with parameter 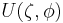 .
.
Given a sample  of size n > 2, the maximum-likelihood equation
of size n > 2, the maximum-likelihood equation
can be solved by a simple fixed-point iteration:
starting with 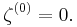 The sequence of likelihood values is non-decreasing, and the solution is unique for samples containing at least three distinct values. [15]
The sequence of likelihood values is non-decreasing, and the solution is unique for samples containing at least three distinct values. [15]
The maximum-likelihood estimate for the median (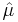 ) and scale parameter (
) and scale parameter (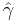 ) of a real Cauchy sample is obtained by the inverse transformation:
) of a real Cauchy sample is obtained by the inverse transformation:
For n ≤ 4, closed-form expressions are known for 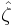 .[10] The density of the maximum-likelihood estimator at
.[10] The density of the maximum-likelihood estimator at  in the unit disk is necessarily of the form:
in the unit disk is necessarily of the form:
where
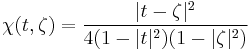 .
.
Formulae for 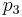 and
and 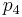 are available.[16]
are available.[16]
Multivariate Cauchy distribution
A random vector X = (X1, ..., Xk)′ is said to have the multivariate Cauchy distribution if every linear combination of its components Y = a1X1 + ... + akXk has a Cauchy distribution. That is, for any constant vector a ∈ Rk, the random variable Y = a′X should have a univariate Cauchy distribution.[17] The characteristic function of a multivariate Cauchy distribution is given by:
where 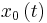 and
and 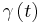 are real functions with
are real functions with 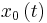 a homogeneous function of degree one and
a homogeneous function of degree one and 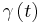 a positive homogeneous function of degree one.[17] More formally:[17]
a positive homogeneous function of degree one.[17] More formally:[17]
 and
and 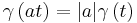 for all t.
for all t.
An example of a bivariate Cauchy distribution can be given by:[18]
Note that in this example, even though there is no analogue to a covariance matrix, x and y are not statistically independent.[18]
Analogously to the univariate density, the multidimensional Cauchy density also relates to the Multivariate Student distribution. They are equivalent when the degrees of freedom parameter is equal to one. The density of a k dimension Student distribution with one degree of freedom becomes:
Properties and details for this density can be obtained by taking it as a particular case of the Multivariate Student density.
Transformation properties
- If
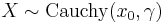 then
then 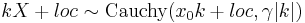
- If
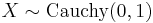 then
then 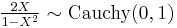
- If
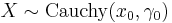 and
and 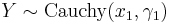 are independent, then
are independent, then 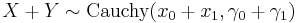
- If
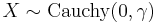 then
then 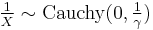
- McCullagh's parametrization of the Cauchy distributions: Expressing a Cauchy distribution in terms of one complex parameter
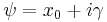 , define X ~ Cauchy
, define X ~ Cauchy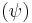 to mean X ~ Cauchy
to mean X ~ Cauchy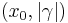 . If X ~ Cauchy
. If X ~ Cauchy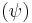 then:
then:
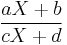 ~ Cauchy
~ Cauchy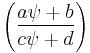 where a,b,c and d are real numbers.
where a,b,c and d are real numbers.
- Using the same convention as above, if If X ~ Cauchy
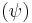 then:
then:
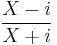 ~ CCauchy
~ CCauchy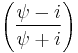
- where "CCauchy" is the circular Cauchy distribution.
Related distributions
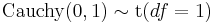 Student's t distribution
Student's t distribution- If
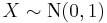 and
and 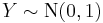 then
then 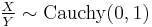
- If
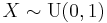 then
then 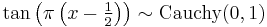
- If
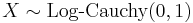 then
then 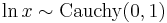
- The Cauchy distribution is a limiting case of a Pearson distribution of type 4
- The Cauchy distribution is a special case of a Pearson distribution of type 7
- The Cauchy distribution is a stable distribution: if X ~ Stable
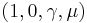 , then X ~Cauchy(μ, γ).
, then X ~Cauchy(μ, γ). - The Cauchy distribution is a singular limit of a Hyperbolic distribution
- The wrapped Cauchy distribution, taking values on a circle, is derived from the Cauchy distribution by wrapping it around the circle.
Relativistic Breit–Wigner distribution
In nuclear and particle physics, the energy profile of a resonance is described by the relativistic Breit–Wigner distribution, while the Cauchy distribution is the (non-relativistic) Breit–Wigner distribution.
See also
References
- ^ http://webphysics.davidson.edu/Projects/AnAntonelli/node5.html Note that the intensity, which follows the Cauchy distribution, is the square of the amplitude.
- ^ E. Hecht (1987). Optics (2nd ed.). Addison-Wesley. p. 603.
- ^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model". Journal of Econometrics (Elsevier): 219–230. http://www.econ.yorku.ca/cesg/papers/berapark.pdf. Retrieved 2011-06-02.
- ^ Vasicek, Oldrich (1976). "A Test for Normality Based on Sample Entropy". Journal of the Royal Statistical Society, Series B (Methodological) 38 (1): 54–59.
- ^ S.Kotz et al (2006). Encyclopedia of Statistical Sciences (2nd ed.). John Wiley & Sons. p. 778. ISBN 978-0-471-15044-2.
- ^ Cane, Gwenda J. (1974). "Linear Estimation of Parameters of the Cauchy Distribution Based on Sample Quantiles". Journal of the American Statistical Association 69 (345): 243–245. JSTOR 2285535.
- ^ Zhang, Jin (2010). "A Highly Efficient L-estimator for the Location Parameter of the Cauchy Distribution". Computational Statistics 25 (1): 97–105. http://www.springerlink.com/content/3p1430175v4806jq.
- ^ a b Rothenberg, Thomas J.; Fisher, Franklin, M.; Tilanus, C.B. (1966). "A note on estimation from a Cauchy sample". Journal of the American Statistical Association 59 (306): 460–463.
- ^ a b c d Bloch, Daniel (1966). "A note on the estimation of the location parameters of the Cauchy distribution". Journal of the American Statistical Association 61 (316): 852–855. JSTOR 2282794.
- ^ a b c Ferguson, Thomas S. (1978). "Maximum Likelihood Estimates of the Parameters of the Cauchy Distribution for Samples of Size 3 and 4". Journal of the American Statistical Association 73 (361): 211. JSTOR 2286549.
- ^ Cohen Freue, Gabriella V. (2007). "The Pitman estimator of the Cauchy location parameter". Journal of Statistical Planning and Inference 137: 1901. http://faculty.ksu.edu.sa/69424/USEPAP/Coushy%20dist.pdf.
- ^ Barnett, V. D. (1966). "Order Statistics Estimators of the Location of the Cauchy Distribution". Journal of the American Statistical Association 61 (316): 1205. JSTOR 2283210.
- ^ McCullagh, P., "Conditional inference and Cauchy models", Biometrika, volume 79 (1992), pages 247–259. PDF from McCullagh's homepage.
- ^ K.V. Mardia (1972). Statistics of Directional Data. Academic Press.
- ^ J. Copas (1975). "On the unimodality of the likelihood function for the Cauchy distribution". Biometrika 62: 701–704.
- ^ P. McCullagh (1996). "Mobius transformation and Cauchy parameter estimation.". Annals of Statistics 24: 786–808. JSTOR 2242674.
- ^ a b c Ferguson, Thomas S. (1962). "A Representation of the Symmetric Bivariate Cauchy Distribution". Journal of the American Statistical Association: 1256. JSTOR 2237984.
- ^ a b Molenberghs, Geert; Lesaffre, Emmanuel (1997). "Non-linear Integral Equations to Approximate Bivariate Densities with Given Marginals and Dependence Function". Statistica Sinica 7: 713–738. http://www3.stat.sinica.edu.tw/statistica/oldpdf/A7n310.pdf.
External links
- Earliest Uses: The entry on Cauchy distribution has some historical information.
- Weisstein, Eric W., "Cauchy Distribution" from MathWorld.
- GNU Scientific Library – Reference Manual
|
|||||||||||
![f(x; x_0,\gamma) = \frac{1}{\pi\gamma \left[1 %2B \left(\frac{x - x_0}{\gamma}\right)^2\right]}
= { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 %2B \gamma^2 } \right],](/2012-wikipedia_en_all_nopic_01_2012/I/c20c295d95a9bb416922020313ac0331.png)
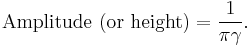
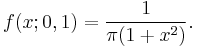
![f(x; x_0,\gamma,I) = \frac{I}{\left[1 %2B \left(\frac{x-x_0}{\gamma}\right)^2\right]}
= { I }\left[ { \gamma^2 \over (x - x_0)^2 %2B \gamma^2 } \right],](/2012-wikipedia_en_all_nopic_01_2012/I/2aef4c7925efc40796a83c44e4350ff7.png)

![Q(p; x_0,\gamma) = x_0 %2B \gamma\,\tan\left[\pi\left(p-\tfrac{1}{2}\right)\right].](/2012-wikipedia_en_all_nopic_01_2012/I/971ef3b71572a04317d498448355a605.png)
![Q'(p; \gamma) = \gamma\,\pi\,{\sec}^2\left[\pi\left(p-\tfrac{1}{2}\right)\right].\!](/2012-wikipedia_en_all_nopic_01_2012/I/c4fa70133f7e8adbbc92a7202577ad65.png)
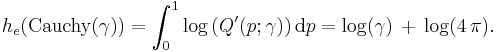
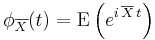
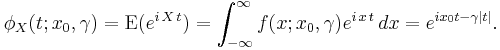
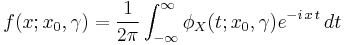
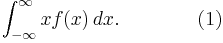
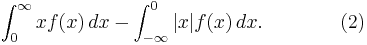
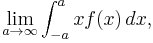
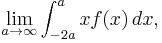
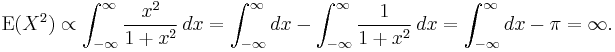
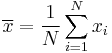
![\hat\ell(\!x_0,\gamma|\,x_1,\dots,x_n) = n \log (\gamma) - \sum_{i=1}^n (\log [(\gamma)^2 %2B (x_i - \!x_0)^2]) - n \log (\pi)](/2012-wikipedia_en_all_nopic_01_2012/I/db467f69b0f12ea1daa2c776c5b6ced4.png)
![\sum_{i=1}^n (x_i - \!x_0) / (\gamma^2 %2B [x_i - \!x_0]^2) = 0](/2012-wikipedia_en_all_nopic_01_2012/I/40db2b2019581dd05ce4f2fee4614f60.png)
![\sum_{i=1}^n \gamma^2 / (\gamma^2 %2B [x_i - \!x_0]^2) - n/2 = 0](/2012-wikipedia_en_all_nopic_01_2012/I/6891977a7e8d8f6cff043a7ec679d287.png)
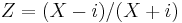
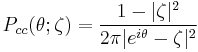
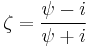
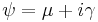
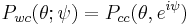
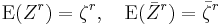
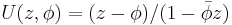
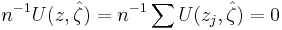
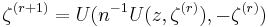
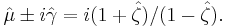
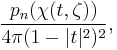
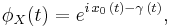
![f(x, y; x_0,y_0,\gamma)= { 1 \over \pi } \left[ { \gamma \over ((x - x_0)^2 %2B (y - y_0)^2 %2B\gamma^2)^{1.5} } \right] .](/2012-wikipedia_en_all_nopic_01_2012/I/b657f1f3449844fd00efa30e769743cf.png)
![f( {\mathbf x}�; {\mathbf\mu},{\mathbf\Sigma}, k)= \frac{\Gamma\left[(1%2Bk)/2\right]}{\Gamma(1/2)\pi^{k/2}\left|{\mathbf\Sigma}\right|^{1/2}\left[1%2B({\mathbf x}-{\mathbf\mu})^T{\mathbf\Sigma}^{-1}({\mathbf x}-{\mathbf\mu})\right]^{(1%2Bk)/2}} .](/2012-wikipedia_en_all_nopic_01_2012/I/064cec34e2ac209fde860864580c26bb.png)